Keskaegse matemaatiku Leonardo Fibonacci probleem küülikutega

Vaatame, kuidas küülikute arv esimese kuue kuu jooksul kasvab:

1. kuu. Üks noor küülikute paar.

2. kuu. Üks originaalpaar on endiselt. Küülikud pole veel sünnitusikka jõudnud.

3. kuu. Kaks paari: algne, sünnitusealine vanus + paar küülikuid, kelle ta sünnitas.

4. kuu. Kolm paari: üks originaalpaar + üks küülikupaar, kelle ta kuu alguses sünnitas + üks küülikupaar, kes sündisid kolmandal kuul, kuid pole veel suguküpseks saanud.

5. kuu. Viis paari: üks originaalpaar + üks paar, kes on sündinud kolmandal kuul ja jõudnud viljakas vanusesse + kaks uut paarid, kellele nad sünnitasid, + üks paar, kes sündis neljandal kuul, kuid pole veel jõudnud küpsus.

6. kuu. Kaheksa paari: viis paari eelmisest kuust + kolm vastsündinud paari. Jne.

Selguse huvides kirjutame saadud andmed tabelisse:

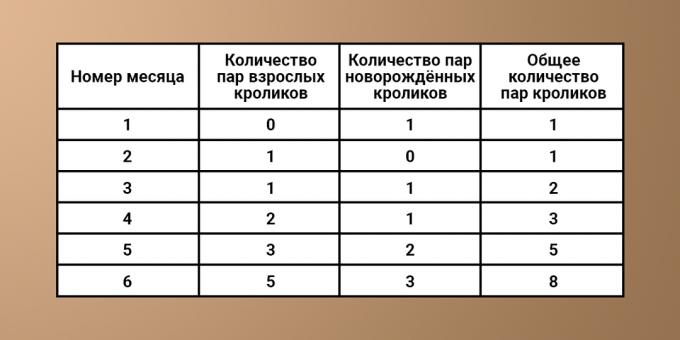
Kui uurite tabelit hoolikalt, saate tuvastada järgmise mustri. Iga kord, kui n-ndal kuul viibivate küülikute arv on võrdne küülikute arvuga eelmisel kuul (n - 1), summeerituna vastsündinud küülikute arvuga. Nende arv on omakorda võrdne loomade koguarvuga (n - 2) kuu seisuga (mis oli kaks kuud tagasi). Siit saate järeldada

valem:

F_n = F_{n - 1}+ F_{n - 2},

kus F_n - küülikupaaride koguarv n-ndal kuul, F_{n - 1} On küülikupaaride koguarv eelmisel kuul ja F_{n - 2} - küülikupaaride koguarv kaks kuud tagasi.

Loendame seda kasutades loomade arvu järgnevatel kuudel:

7. kuu. 8 + 5 = 13.

8. kuu. 13 + 8 = 21.

9. kuu. 21 + 13 = 34.

10. kuu. 34 +21 = 55.

11. kuu. 55 + 34 = 89.

12. kuu. 89 + 55 = 144.

13. kuu (järgmise aasta algus). 144 + 89 = 233.

13. kuu alguses, see tähendab aasta lõpus, on meil 233 paari küülikuid. Neist 144 paari on täiskasvanud ja 89 noored. Saadud järjestus 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 helistas Fibonacci numbritele. Selles on iga uus lõplik arv võrdne summa kaks eelmist.